Fibonacci Sequence in Art – Using the Fibonacci Theory in Art
You may have heard of the golden section in your mathematics class or perhaps referred to as the golden ratio, but have you heard of the Fibonacci sequence? The Fibonacci sequence is closely connected to the golden ratio and frequently occurs in various facets of human life. From nature to space and art, the Fibonacci sequence discussed below is the formula to remember! Below is an article that will take you on a journey into the Fibonacci sequence in art as well as answer questions such as “why is the Fibonacci sequence so important?”
Table of Contents
- 1 What Is the Fibonacci Sequence?
- 2 Application of the Fibonacci Theory
- 3 Frequently Asked Questions
- 3.1 Why Is the Fibonacci Sequence So Important?
- 3.2 What Is the Fibonacci Sequence Used For?
- 3.3 What Is the Difference Between the Golden Ratio and the Fibonacci Sequence?
- 3.4 What Is the Formula for Calculating the Value of the Golden Ratio?
- 3.5 What Makes the Fibonacci Spiral Different From the Golden Spiral?
- 3.6 Who Coined the Golden Ratio Method?
What Is the Fibonacci Sequence?
Each object and person in the universe is made up of a unique design, including yourself if you consider that no two people share the exact same DNA makeup. Commonly referred to as “nature’s code”, the Fibonacci sequence finds itself at the center of most foundational facets of human existence, including popular culture.
First documented in 300 BC by Greek mathematician Euclid, the Fibonacci sequence is a mathematical formula that suggests that each number is equal to the sum of the two numbers that precede it.
Numerically, the sequence starts with the integers 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on, continuing up to infinity! The sequence begins with a zero, followed by a one, another one, and by the fourth digit, the sequence begins by adding the last one to the two to arrive at three.
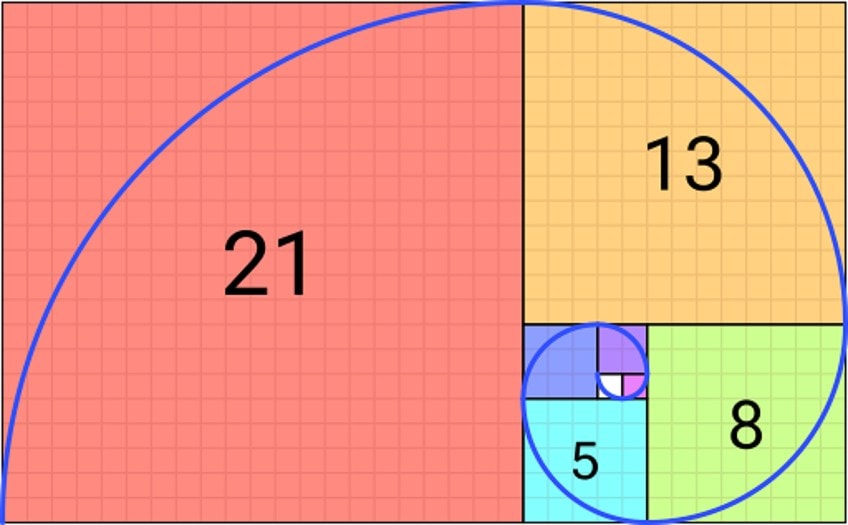
Although this may be confusing to some at first, as you take a look at the visual representation of the Fibonacci sequence, you will recognize this as the golden ratio (also referred to as the divine ratio). The golden ratio (1:1.16), as visualized by the golden curve, is an ancient symbol that has possibly existed since the beginning of time.
The golden ratio is mostly used in design and is derived from the Fibonacci sequence to produce aesthetic visuals through proportion across art, graphic design, and architecture.
https://www.youtube.com/watch?v=X5z8OsSeUl8
While the exact origination of the Fibonacci sequence is still under debate, multiple sources state that the formula was possibly discovered by the Italian mathematician Leonardo Fibonacci well after 1170 AD. On the other hand, popular British mathematician, Keith Devlin, states that there are findings dating back to 200 BC consisting of texts within Hindu-Arabic numerical systems and Sanskrit writings which predate the so-called discovery made by Fibonacci.
A text published by Fibonacci titled “Liber Abaci”, also called the “Book of Calculus”, featured methods for calculating and tracking finances, for use by traders, using the Fibonacci sequence.
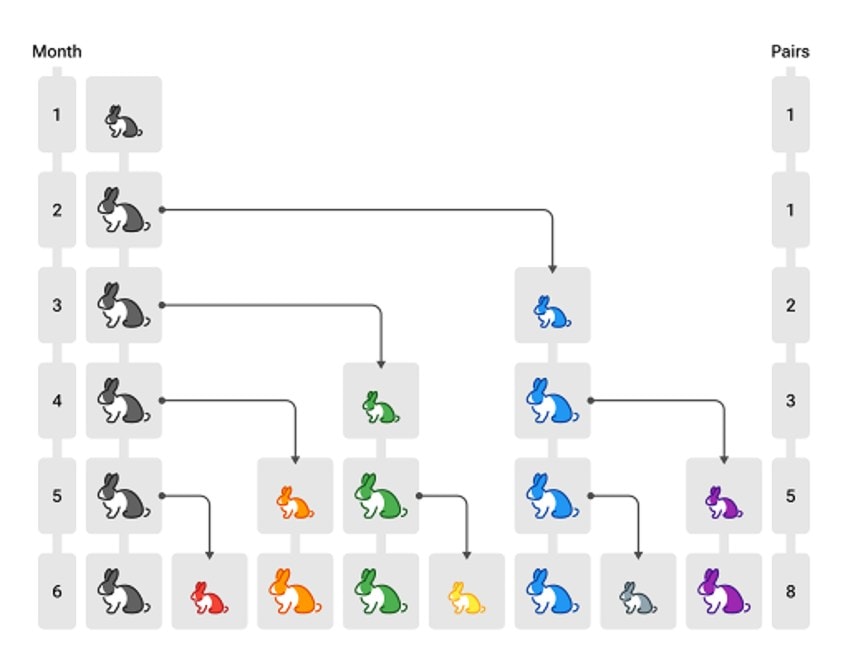
Leonardo of Pisa used an example of rabbits where if you couple two rabbits, one female and one male, and leave the rabbits to reproduce, it will result in one female and one male appearing again in the litter. Using the male and female from the first litter, if those rabbits reproduce – you are left with another litter containing another set of male-female rabbits. The cycle repeats itself and after one year, you are left with around 144 rabbits.
The formula applied to that result is of course none other than the Fibonacci sequence.
What Is the Fibonacci Sequence Used For?
Fibonacci numbers seem to appear in multiple areas of human existence, from orbital systems and plants to tree branches, artichokes, and pine cones. The Fibonacci sequence can also be in the pattern in which sunflowers generate new cells for seeds and even in our own solar system, where the Fibonacci series is used to determine the distances of moons of certain planets such as Saturn, Jupiter, and Uranus. So why is the Fibonacci sequence so important?
The importance of the Fibonacci sequence lies in the very reason why it is a topic of high debate.
Among the reasons, the one that comes to the forefront is the fact that this formula, initially thought to be exclusive to mathematics, became a formula with a ratio that appears in very specific elements in nature; plants, seed growth, and the human ear, and may be considered a universal formula.
Most evidently captured on the petals of flowers, the Fibonacci theory in the application of flowers shows that the petals of certain flowers are equal to that of the different Fibonacci numbers. The Fibonacci theory can also be seen a little more in-depth regarding flowers, cauliflowers, pineapples, and bananas. Here we refer to the Fibonacci spiral defined by the organization of seeds growing on flower heads in a spiral shape.
The Fibonacci order remains a topic of high debate but is still very much reliable in its mathematical basis.
It is only the speculations and hypotheses drawn from the reasoning behind why the sequence appears in many vital aspects of human life that it becomes a subject of debate. To further build on the appearance of the Fibonacci order, there exists the golden angle. The golden angle suggests that the angle at which the new growth occurs from the previous growth sits at 222.5 degrees and divides a 360-degree circle as per the golden section, which is 0.168…
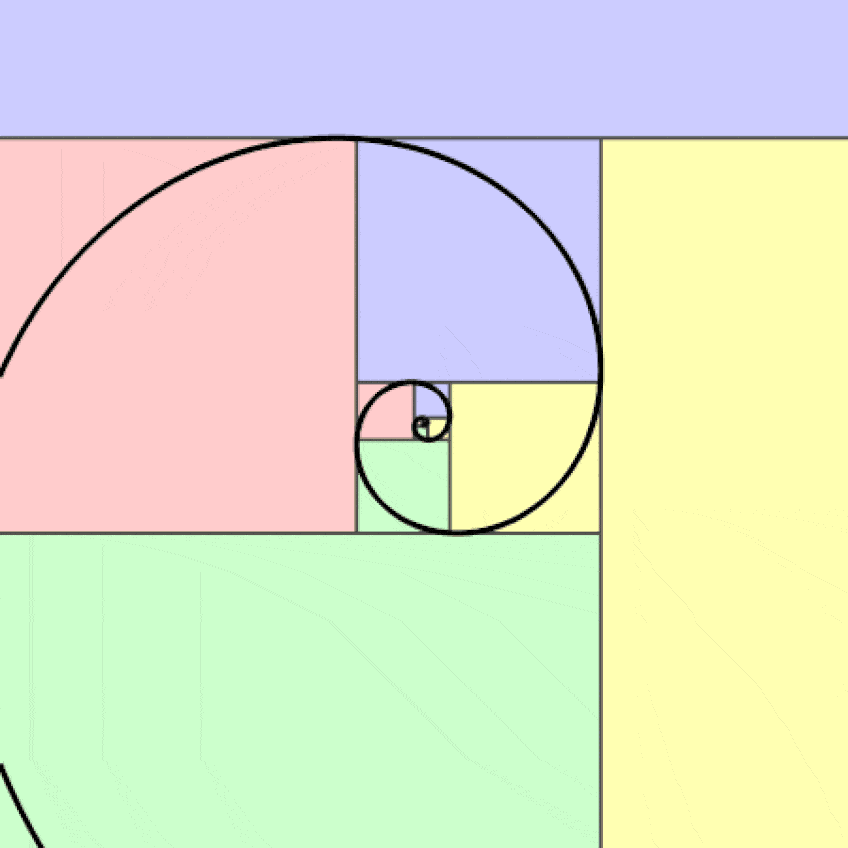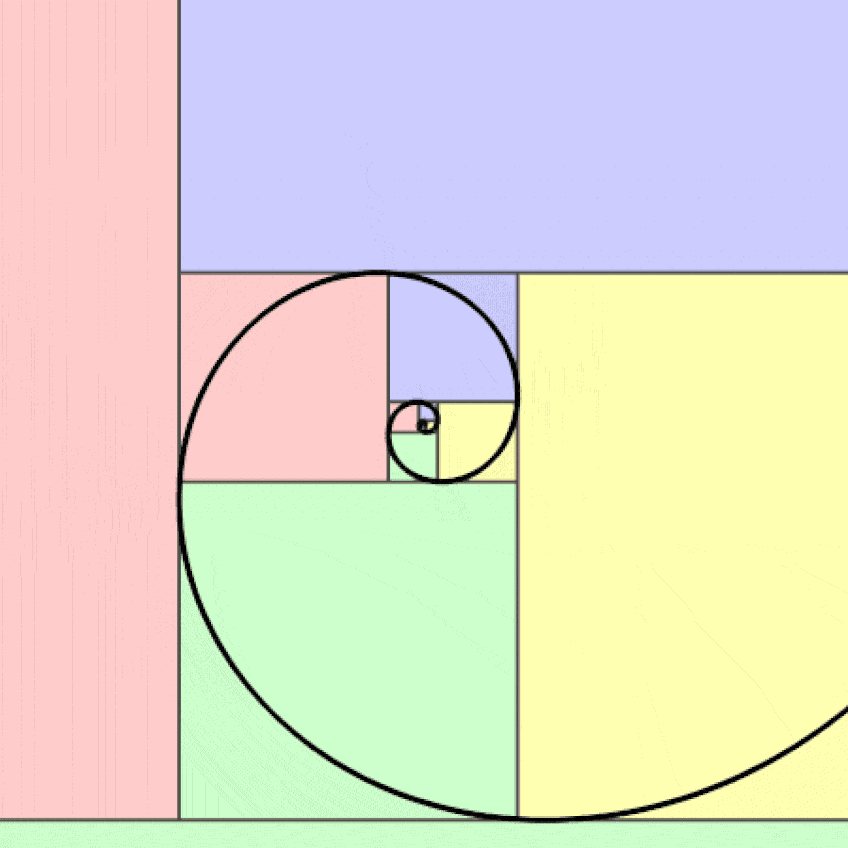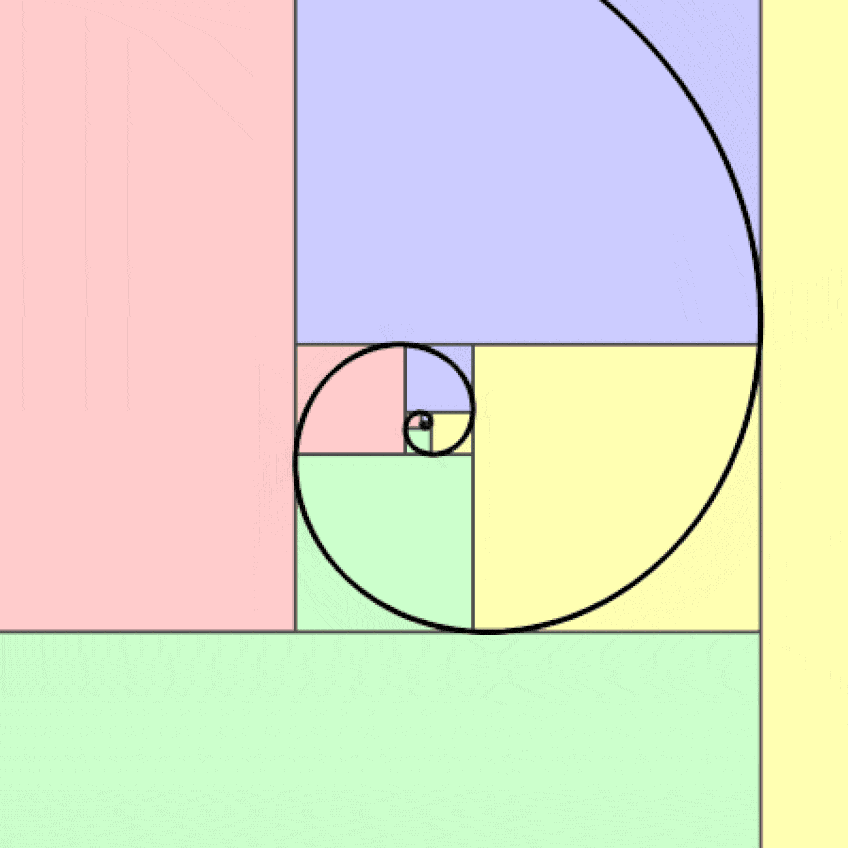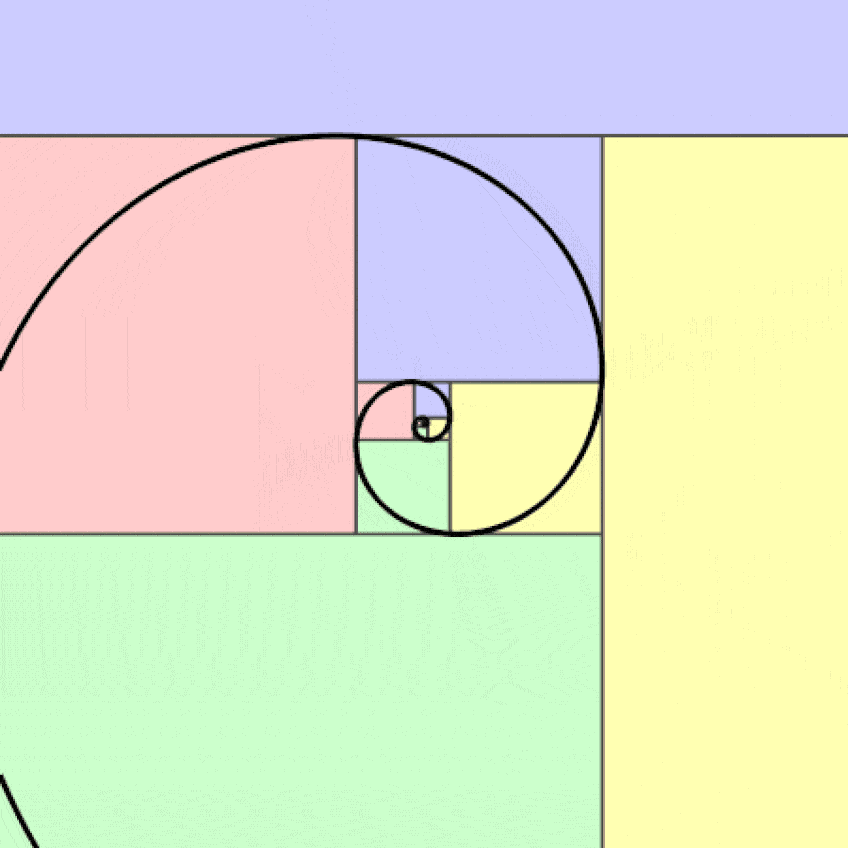
The Rule of Thirds
The rule of thirds speaks directly to a simplified version of the golden ratio where a similar approach to producing an aesthetically pleasing image is possible. From photography to painting, the rule of thirds is applied within the context of composition. To proceed with applying the rule of thirds, you would first divide your image into a grid of three by three and then place the focal point of your image or painting either two-thirds to the left or right for a horizontal image.
The rule of thirds can become complex, but trust your eye for symmetry and you cannot go wrong! If you get stuck, there are photographic editing software programs such as Adobe Lightroom that feature a golden ratio overlay as a guide to help you perfect your composition.
Application of the Fibonacci Theory
While it is useful to draw from the great masters, it can also be just as informative to take a closer look at some of the creative ways in which modern contemporaries have used the Fibonacci sequence over the course of the history of art.
Here are a few examples of the Fibonacci sequence as practiced in art history to inspire your venture into the intersection between mathematics and art.
Examples of the Fibonacci Sequence in Art
According to neuroscientific insights, the human eye can identify symmetry within 0.05 seconds and suggests that symmetry, an aspect of visual aesthetics within the arts, is somewhat of an inherent ability to all. It is the desire for harmonious visual appeal that has informed many of the great artworks of today.
Doryphoros (c. 450 – 440 BC) by Polykleitos
| Artist | Polykleitos |
| Date | c. 450-440 BC |
| Dimensions (cm) | 212 |
| Medium | Marble |
| Where It Is Housed | Naples National Archaeological Museum, Naples, Italy |
One such example in art that draws attention to symmetry is found in a classical marble sculpture of a spear-bearer, titled Doryphoros, sculpted by Greek sculptor Polykleitos around 450-440 BCE. Polykleitos, commonly referred to as “the Elder”, elegantly displayed his eye for symmetry as showcased in the spear-bearer.
It can be said that Polykleitos’ attention to the notion of portraying the perfect proportion of the human body was an expression of beauty.
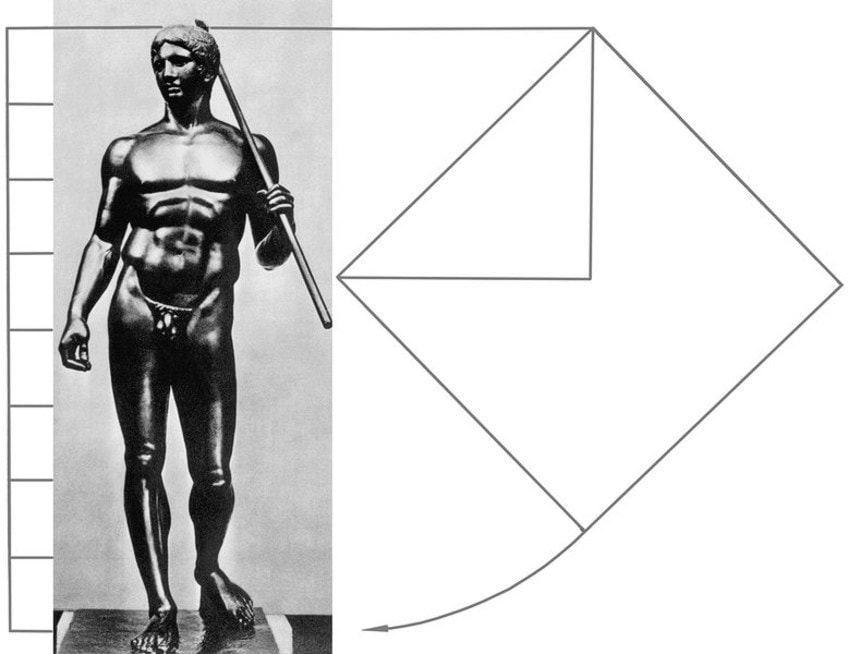
Doryphoros by Polykleitos is one of the most sophisticated examples of art that incorporates the idea of mathematics into the depiction of the human form, using perfection in composition as a measure of “good art”.
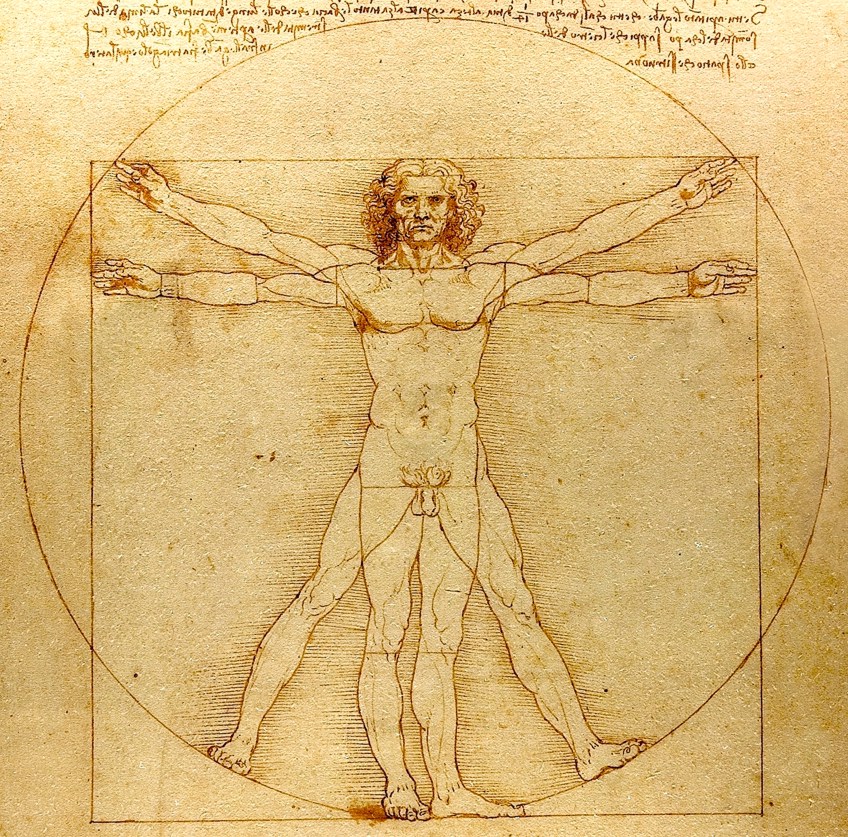
This sculpture also predates “The Vitruvian Man” (c. 1490) by Leonardo da Vinci by almost a thousand years, thus absolving the idea that da Vinci was the first and only individual to propel “golden thinking”.
The School of Athens (c. 1509 – 1511) by Raphael
| Artist | Raffaello Sanzio da Urbino |
| Date | c. 1509-1511 |
| Dimensions (cm) | 500 x 770 |
| Medium | Oil painting |
| Where It Is Housed | Apostolic palace, Vatican City, Rome |
Another artist of the Italian Renaissance who used the Fibonacci sequence in art is Raffaello Sanzio da Urbino (1483-1520), better known as Raphael, whose works were a direct reference to the use of the golden ratio in painting. Alongside the likes of prestigious artists such as Leonardo da Vinci and Michelangelo, Raphael produced an exquisitely composed fresco, The School of Athens (1509-1511), situated in Stanze di Raffaello of the Vatican.
Strategically placed in the middle of the painting sits a golden rectangle, indicating a potential reference to the artist’s use of the golden ratio in composition.
Raphael’s works speak for themselves through the detail and accuracy with which he paints key portions of the fresco. The School of Athens is definitely a prime example highlighting the almost hyperfocus of the great masters on beauty and perfectionism post-humanism.
Piet Mondrian and the Golden Spiral
Famous for his abstract paintings, Dutch artist Pieter Cornelis Mondriaan (1872-1944), created these colorful works of art, which upon first glance may appear to be random rectangles and squares. By now, you should have guessed – Mondrian did well to incorporate the golden curve into his works spanning 1918 to 1938.
An example of this can be seen in his 1921 painting, “Composition with Large Red Plane, Yellow, Black, Gray and Blue”.
Ivan Black and the Square Wave
London-born sculptor Ivan Black applied the Fibonacci sequence to the spectacular Square Wave sculptures, which when in motion, as per natural occurrence, gravity, and movement of the holder, shift to deliver various “organized movements”. These mobile sculptures, created in 2022, are referred to as kinetic artwork, which integrates the complexities of a highly calibrated material with “natural forms” such as the square to deliver an innovative experience.
Such intricacy and precision, as expected of a fusion between the mathematical universe and artistic expression.
Other Examples of the Fibonacci Sequence
In addition to art, the Fibonacci spiral can also be found in many other areas of study. Leonardo da Vinci famously wrote a book on the divine proportions of the golden ratio in various disciplines, and in addition to this, the Fibonacci theory can also be applied to music, architecture, and even the human body! Let’s take a look.
De Divina Proportione and Leonardo da Vinci
A keen collaborator with Leonardo da Vinci, Luca Pacioli wrote a book called De Divina Proportione (1509), which detailed the collaborative insights and findings of the application of the golden ratio in various disciplines. The duo applied their mathematical and creative knowledge across the alphabet, architecture, structures, and even geometric figures.
Da Vinci is one of the primary pioneers of incorporating the divine proportion into some of the most iconic paintings in the world.
Among many of his artworks are The Last Supper (1494-1498) and La Jaconde, better known as the Mona Lisa (1503-1506). Locating the golden ratios in The Last Supper appears much more clear-cut than that of the Mona Lisa. The positioning of the Mona Lisa’s head, neckline, garment, and arm indicate some use of the golden ratio.
Although unclear, it can still be said that the breadth of her face could be very close to the golden ratio of the canvas width.
The Fibonacci Spiral and Music
In addition to the visual applied arts, the occurring Fibonacci order finds itself in music. Fibonacci numbers can be found within one of the core melodic units, the octave. If you are familiar with the octave on a piano, you will find that the octave consists of 13 notes with five black keys and eight white. The fifth note on a scale is also note number eight of 13 notes, thus forming the octave. If you had to divide eight by 13…you are spot on! The result is approximately 0.61538… Coincidence or order?
Even one of the greatest musical talents in music history, Wolfgang Amadeus Mozart, replicated the golden ratio through the arrangement of his piano sonatas. The octave, as referred to in musical terms, is a fundamental component of music known as a “unique interval” that informs the basis of how one writes and interprets music.
How fitting is it that the octave, a foundational musical unit, correlates with one of the most versatile formulae?
The Golden Ratio in Relation to Architecture
The golden ratio can be found within the constructs of important architectural sites across the globe. These include the Parthenon of Greece and the United Nations Secretariat Building located in New York. It is even said that the golden ratio was applied to the construction of the Great Pyramids of Giza.
Other sites where the golden ratio has been found within architecture include the Taj Mahal, the Notre Dame, and even the Eiffel Tower.
The golden ratio in general when applied to architecture is particularly useful in determining an appropriate yet balanced proportion of windows, doors, layout, and the relativity of the sizes to the roof pitch to draft an attractive building or home.
One Step Further: Traces of Fibonacci on the Human Body
You have seen examples of the Fibonacci sequence applied across photography, painting, sculpture, and even music, but is it a stretch to find the traces of the Fibonacci theory in yourself? Not at all. The golden spiral can easily be identified in the shape of the human ear, the cochlea, which is biologically intriguing if the same can be found on flowering heads.
Numerically, as distance is recorded on a planetary level between spatial objects, so too can distance and Fibonacci numbers be connected back to the human hand.
With two hands, each with five fingers divided into three segments with two knuckles each for joining. All of which are Fibonacci numbers. If that is not convincing enough, the length of the bones found on the human arm also equates to Fibonacci numbers.
After deliberating all this information surrounding the Fibonacci sequence, the golden ratio, and its impact across fundamental disciplines, can it be said that beauty is held quite literally in the eye of the beholder? Given that mathematics is a subject carrying immense seriousness and proven fact, it is incredible to find the Fibonacci sequence applied within art. Let this be a glimpse into the vastness of ideas that can emerge from the Fibonacci sequence and hopefully inspire you to delve deeper into the possibilities that incorporating different disciplines can bring to your art practice.
Take a look at our Fibonacci Spiral webstory here!
Frequently Asked Questions
Why Is the Fibonacci Sequence So Important?
There are many reasons why the application of the Fibonacci sequence is so important. The primary reasons include its mathematical and philosophical impact in Europe, which informed the foundation of many famous art pieces you may consider crucial to the discourse of art history. Outside the context of art history, the Fibonacci spiral is also significant as a tool and literal formula that provides a numerical method for expanding the research into multiple scientific fields such as quantum mechanics, coding, cryptography, and physics.
What Is the Fibonacci Sequence Used For?
The Fibonacci sequence is a formula and mathematical reference used to calculate percentages and ratios for use by traders. Alternatively, it is used in various fields such as art, design, music, design, finance, architecture, and even engineering applications and computer data structures. Other uses are found in architectural engineering, audio compression, trading, and financial investments.
What Is the Difference Between the Golden Ratio and the Fibonacci Sequence?
The Fibonacci sequence differs from the golden ratio in that the ratio for interval reduction is not constant. The golden ratio is a result of dividing each figure on the Fibonacci sequence by the preceding number. Mathematically, F(n) refers to the nth term of the Fibonacci sequence and the quotient of F(n)/ F(n-1) is set to approach the limit 1.618 with increasing n values. This limit is called the golden ratio.
What Is the Formula for Calculating the Value of the Golden Ratio?
The formula to calculate the value of the golden ratio is ϕ (phi) = (1+√5) / 2. In design contexts, the golden ratio can be useful in designing logos, shapes, and aesthetic layouts. Design-wise, the golden ratio can be calculated by dividing your line into two parts ensuring the longer line divided by the shorter line equates to the sum of both the parts divided by the long line. If you struggle with the details, you can always make use of an online Golden Ratio calculator.
What Makes the Fibonacci Spiral Different From the Golden Spiral?
The Fibonacci spiral is characterized by a discontinuous curvature with a cyclic varying arm-radius angle while the golden spiral is characterized by the opposite, that being a continuous curvature with a constant arm-radius angle.
Who Coined the Golden Ratio Method?
The first person to describe this formula as the golden ratio was Martin Ohm, a German Mathematician who founded the word goldener schnitt in 1835, now known as the golden section.
Isabella studied at the University of Cape Town in South Africa and graduated with a Bachelor of Arts majoring in English Literature & Language and Psychology. Throughout her undergraduate years, she took Art History as an additional subject and absolutely loved it. Building on from her art history knowledge that began in high school, art has always been a particular area of fascination for her. From learning about artworks previously unknown to her, or sharpening her existing understanding of specific works, the ability to continue learning within this interesting sphere excites her greatly.
Her focal points of interest in art history encompass profiling specific artists and art movements, as it is these areas where she is able to really dig deep into the rich narrative of the art world. Additionally, she particularly enjoys exploring the different artistic styles of the 20th century, as well as the important impact that female artists have had on the development of art history.
Learn more about Isabella Meyer and the Art in Context Team.
Cite this Article
Isabella, Meyer, “Fibonacci Sequence in Art – Using the Fibonacci Theory in Art.” Art in Context. July 15, 2022. URL: https://artincontext.org/fibonacci-sequence-in-art/
Meyer, I. (2022, 15 July). Fibonacci Sequence in Art – Using the Fibonacci Theory in Art. Art in Context. https://artincontext.org/fibonacci-sequence-in-art/
Meyer, Isabella. “Fibonacci Sequence in Art – Using the Fibonacci Theory in Art.” Art in Context, July 15, 2022. https://artincontext.org/fibonacci-sequence-in-art/.
